Binary Search Tree 二叉搜索树

简称 BST，也称二叉排序树或二叉查找树。

特点：

任一结点 > 其左子树的所有结点，
并且< 其右子树的所有结点；
结点的左、右子树，也是二叉排序树；
每个结点键值唯一（不能重复）

重要性质：

中序遍历二叉排序树得到递增序列

所以判断 1 棵二叉树是否是二叉排序树？
只要中序遍历，得到递增序列才是。

插入

若当前树为空，则新结点为根
若当前树不空，
将待插入 x 与根比较；
- 若 x 等于根，不用插入
- 若 x 大于根，则去右子树 (找位置)；
- 若 x 小于根，则去左子树 (找位置)；

可以总结为：

插入之前，先查找：

若找到，不用插入
若找不到，则在到达的空位置处，放入 x；

所以最新插入的结点，一定是叶子；

func insertIntoBST(root *TreeNode, val int) *TreeNode {
	if root == nil {
		return &TreeNode{
			Val: val,
		}
	}
	if root.Val > val {
		root.Left = insertIntoBST(root.Left, val)
	}
	if root.Val < val {
		root.Right = insertIntoBST(root.Right, val)
	}
	return root
}

查找

从根结点开始，如果树为空，则返回 NULL
如果非空，从根结点开始，比较待检索的键值
- 若相等，则成功；
- 若小于根，
  则去根的左子树；
- 若大于根，
  则去根的右子树，

迭代

func searchBST(root *TreeNode, val int) *TreeNode {
	for root != nil {
		if root.Val > val {
			root = root.Left
		} else if root.Val < val {
			root = root.Right
		} else {
			return root
		}
	}
	return nil
}

删除

考虑三种情况：

① 要删除叶子结点
直接删除，并将父结点指针置为 NULL

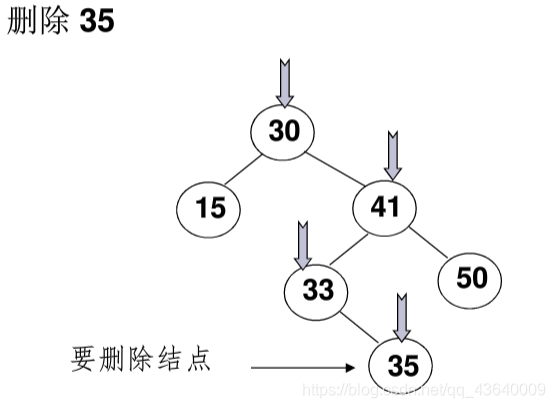
② 删除只有 1 个孩子的结点
将父结点指针指向要删除结点的孩子结点

③ 删除有左右子树的结点
用另一个结点替代删除的结点：
- 右子树的最小元素或者左子树的最大元素

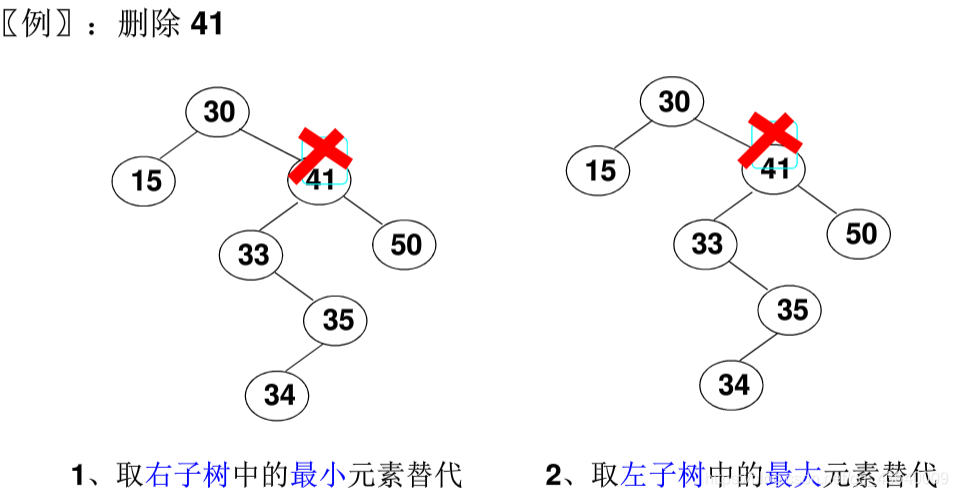
func deleteNode(root *TreeNode, key int) *TreeNode {
	if root == nil {
		return root
	}
	if root.Val > key {
		root.Left = deleteNode(root.Left, key)
		return root
	}
	if root.Val < key {
		root.Right = deleteNode(root.Right, key)
		return root
	}
	// 情况 1 : 以下两个 if 已经处理
	if root.Left == nil { // 情况 2 左
		return root.Right
	}
	if root.Right == nil { // 情况 2 右
		return root.Left
	}
	// 情况 3 ： 使用右子树最小元素
	minNode := root.Right
	for minNode.Left != nil {
		minNode = minNode.Left
	}
	root.Val = minNode.Val
	root.Right = deleteNode(root.Right, minNode.Val)
	return root
}

平均检索长度 ASL

比较次数：不大于树的深度

最坏平均查找长度 ASL：(n+1)/2

最好 ASL：$log2(n)$ (参考二分查找)

所有操作的复杂度都是 $O(logn)$